Over 1.096.000 registered users (EN+CZ).
AutoCAD tips, Inventor tips, Revit tips.
Try the new precise Engineering calculator and the updated Barcode generator.
New AutoCAD 2026 commands and variables.
 Discussion forum
Discussion forum
?CAD discussions, advices, exchange of experience
 CAD discussion forum - ask any CAD-related questions here, share your CAD knowledge on AutoCAD, Inventor, Revit and other Autodesk software with your peers from all over the world. To start a new topic, choose an appropriate forum.
CAD discussion forum - ask any CAD-related questions here, share your CAD knowledge on AutoCAD, Inventor, Revit and other Autodesk software with your peers from all over the world. To start a new topic, choose an appropriate forum.
Please abide by the rules of this forum.
This is a peer-to-peer forum. The forum doesn't replace the official direct technical support provided by ARKANCE for its customers.
How to post questions: register or login, go to the specific forum and click the NEW TOPIC button.
|
Post Reply 
|
| Author | |
wtojp2013 
Newbie 
Joined: 21.Oct.2013 Location: Hong Kong Using: autocad Status: Offline Points: 8 |
 Topic: Fit Circular Compound Curve Topic: Fit Circular Compound CurvePosted: 29.Jun.2019 at 03:39 |
|
As the coordinates of two tangent points are fixed by some constraints. I would like to fit a circular curves to joint them together. If begin radius say is 80m. How can I find the second radius which shown in attached file ?
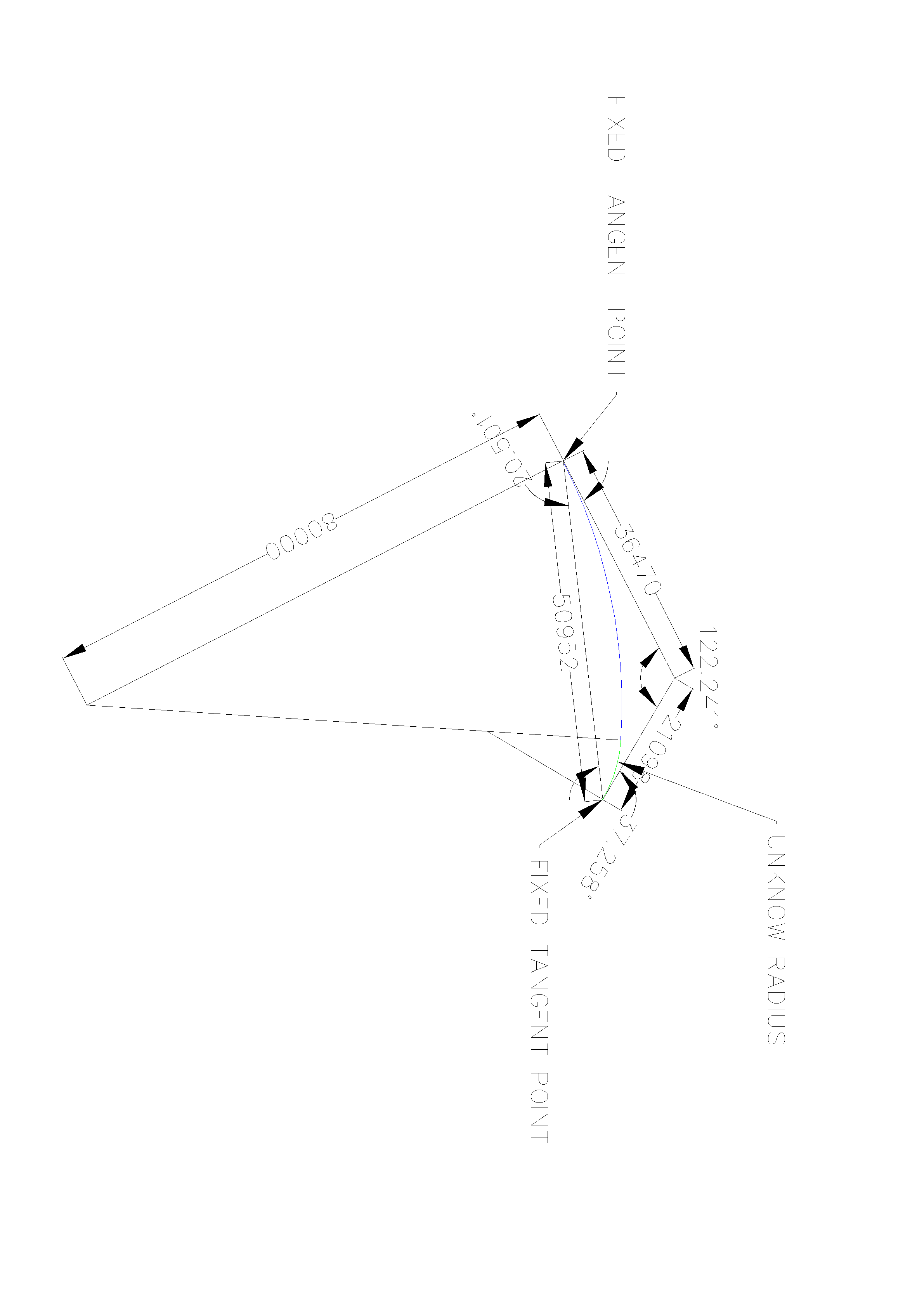 uploads/413380/ACADCCurve-Model.dwg uploads/413380/ACADCCurve-Model.dwg
|
|
 |
|
philippe JOSEPH 
Senior Member 
Joined: 14.Mar.2011 Location: France Using: AutoCAD Mechanical 2017 Status: Offline Points: 1493 |
 Posted: 01.Jul.2019 at 08:51 Posted: 01.Jul.2019 at 08:51 |
|
Hello wtojp2013, I'm afraid some dimensions are missing to find ONE solution.
I can't open the AutoCAD file but if you don't fix the length of the R80000 radius there will be an infinity of "unknown radius". Eventually try PARAMETRIC CONSTRAINTS to do this but you must fix some other dimension( s ). By doing this you must use EXACT angle dimensions or exact length dimensions or intersection positions. Are the basic dimensions : 36470 , 21098 , 50952 and R80000 exact or aproximate ?????? I hope this will help you.
|
|
 |
|
Kent Cooper 
Senior Member 
Joined: 12.Mar.2013 Location: United States Using: AutoCAD2020, 2023 Status: Offline Points: 686 |
 Posted: 01.Jul.2019 at 14:45 Posted: 01.Jul.2019 at 14:45 |
With different lengths of the 80m-radius arc [blue], there would be different tangent continuations from it [green] that would end at the other fixed point, but I think only one that would be tangent to the short leg of the triangle at that point. That's the challenge -- find the angle the blue Arc must swing through so that the the green continuation will end up at the other corner tangent to that short leg. Or, to put it another way, find the radius for the green Arc such that the blue Arc coming tangent to one side from one corner, and the green Arc coming tangent to another side from another corner, will meet tangent to each other. I haven't thought of a solution, but there may be one. [And no, the sizes shown, both lengths and angles, are not precise, but are all rounded, except for the 80m radius of the blue Arc and length of its two radial Lines.]
Edited by Kent Cooper - 01.Jul.2019 at 15:00 |
|
 |
|
Kent Cooper 
Senior Member 
Joined: 12.Mar.2013 Location: United States Using: AutoCAD2020, 2023 Status: Offline Points: 686 |
 Posted: 01.Jul.2019 at 15:46 Posted: 01.Jul.2019 at 15:46 |
|
Having thought about it some more, I think this is a situation that would require iteration through small adjustments until a result falls within some tolerance.
Given the triangle defining points A/B/C, and a radius for the blue Arc, a routine could find D, and it could determine the dashed yellow from B on which the center of the green Arc must lie. It would then try swinging the D-E angle (magenta variability), at each try calculating F, and comparing the distance F-E with the distance F-B. The solution would be when those are equal within whatever tolerance you need.
Edited by Kent Cooper - 01.Jul.2019 at 16:13 |
|
 |
|
philippe JOSEPH 
Senior Member 
Joined: 14.Mar.2011 Location: France Using: AutoCAD Mechanical 2017 Status: Offline Points: 1493 |
 Posted: 01.Jul.2019 at 20:48 Posted: 01.Jul.2019 at 20:48 |
|
Hello wtojp2013 and Kent, so if the situation needs iteration to have a "informatically correct and not rounded solution" then it might be only with PARAMETRIC CONSTRAINTS the way to get it right.
That's what I tought at once ( and also because I can't have a this moment access to the AutoCAD file ). I have done a "manual CAD" try on a paper and I found that the solution(s) could be all within some values of the R80000 arc length. What we ( only ) need is to place the center of the unknown radius on a line perpendicular to the right fixed tangent point at the crossing to the right line coming from the center of the R80000 radius, in other words : on the line D-E for a center F or on the line D-(E) for a center (F) and this couls allow numberous values between reasonable ones.
|
|
 |
|
Kent Cooper 
Senior Member 
Joined: 12.Mar.2013 Location: United States Using: AutoCAD2020, 2023 Status: Offline Points: 686 |
 Posted: 01.Jul.2019 at 22:37 Posted: 01.Jul.2019 at 22:37 |
Except that at any (E) & (F) location other than the one and only right one, the blue and green Arcs will not be tangent to each other. Maybe it's only my assumption that tangency between the two of them is required, but if not, you're right that it's a comparatively trivial problem. That tangency happens only when distance F-E is equal to F-B, which happens in only one location. It's pretty obvious that (F)-(E) is not the same distance as (F)-B. My parentheses around (E) and (F) were intended to indicate a trial direction, to be checked for that equality, and when unequal, the direction would be adjusted and a new trial checked.
|
|
 |
|
philippe JOSEPH 
Senior Member 
Joined: 14.Mar.2011 Location: France Using: AutoCAD Mechanical 2017 Status: Offline Points: 1493 |
 Posted: 02.Jul.2019 at 12:08 Posted: 02.Jul.2019 at 12:08 |
|
You are right Master Kent, only iteration ( unprecise ) or parametric constraints ( informatically correct ) can give you F-E = F-B.
wtojp2013 are you still alive ?
|
|
 |
|
wtojp2013 
Newbie 
Joined: 21.Oct.2013 Location: Hong Kong Using: autocad Status: Offline Points: 8 |
 Posted: 02.Aug.2019 at 10:34 Posted: 02.Aug.2019 at 10:34 |
|
I am sorry for my late reply. Point A,B,C are Fixed and Radius R1 is floating. If Radius of R1 say 80000, I would like to find point D and Radius R2. Then The distance from center of R2 to point D and point C are Equal .Thank you.
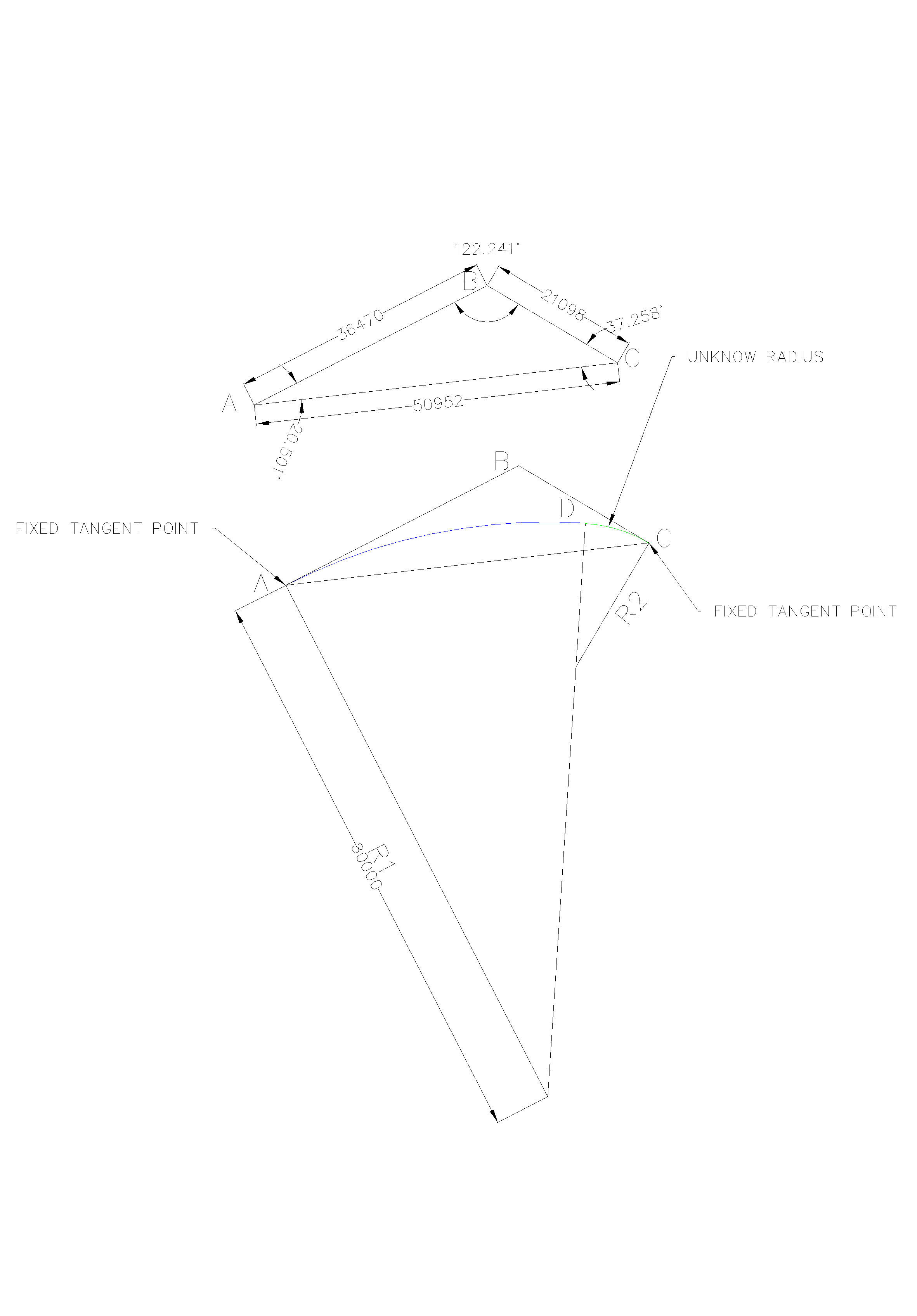 Edited by wtojp2013 - 02.Aug.2019 at 10:43 |
|
 |
|
philippe JOSEPH 
Senior Member 
Joined: 14.Mar.2011 Location: France Using: AutoCAD Mechanical 2017 Status: Offline Points: 1493 |
 Posted: 03.Aug.2019 at 08:18 Posted: 03.Aug.2019 at 08:18 |
|
Hello OK wtojp2013 for the informations but I think that this was already understood by Kent and I.
Can't you follow the instructions of Kent on 01.Jul.2019 at 15:46 ( work by iteration ) or mine on 02.Jul.2019 at 12:08 ( work with parametric constaints ) ?
Edited by philippe JOSEPH - 03.Aug.2019 at 11:55 |
|
 |
|
Post Reply 
|
|
|
Tweet
|
| Forum Jump | Forum Permissions  You cannot post new topics in this forum You cannot reply to topics in this forum You cannot delete your posts in this forum You cannot edit your posts in this forum You cannot create polls in this forum You cannot vote in polls in this forum |
This page was generated in 0,180 seconds.
![CAD Forum - tips, tricks, discussion and utilities for AutoCAD, Inventor, Revit and other Autodesk products [www.cadforum.cz] CAD Forum - tips, tricks, discussion and utilities for AutoCAD, Inventor, Revit and other Autodesk products [www.cadforum.cz]](/common/arkance_186.png)









 Fit Circular Compound Curve
Fit Circular Compound Curve Topic Options
Topic Options philippe JOSEPH wrote:
philippe JOSEPH wrote:


